本文内容可能随时间变动而失效,请以页面显示的更新时间为准。
若内容已不准确或资源失效,欢迎留言或联系站长反馈修正。
⚠️ 免责声明:
本文仅供学习与参考,观点仅代表作者个人意见,与本站无关。
如有侵权问题,请立即联系我们处理,谢谢理解与支持。
堆和栈是计算机内存中的两种不同的数据结构,它们在内存管理和数据存储方面有各自的特点。
栈是一种具有后进先出(LIFO)特性的数据结构。想象一下,栈就像是一摞盘子。最后放上去的盘子会最先被拿走。在计算机中,栈主要用于存储局部变量和函数调用的相关信息。当一个函数被调用时,函数的参数、局部变量以及返回地址等信息都会被压入栈中。函数执行结束后,这些信息会按照后进先出的原则从栈中弹出。栈的内存分配是由系统自动完成的,它的大小在程序运行前通常是固定的,而且栈的内存空间是连续的。如果栈空间不足,就可能会导致栈溢出的错误。
堆则是一种更为灵活的数据存储区域。它用于动态分配内存。就像是在一个大仓库里,你可以根据需要随时申请一块空间来存放东西。程序员可以使用特定的函数(在 C 和 C++ 中是 malloc 和 free,在 Java 中是 new 和 delete)来在堆中分配和释放内存。堆的内存空间不是连续的,而且分配和释放的时间由程序员控制。这就意味着如果程序员不小心,就可能会出现内存泄漏(分配了内存但没有释放)或者悬空指针(释放了内存但仍然使用指向这块内存的指针)等问题。堆的大小通常比栈要大得多,它可以用于存储较大的数据结构,比如大型数组、树、图等复杂的数据结构。
介绍一下链表和数组都有什么区别 ?
链表和数组是两种常见的数据存储结构, 它们有很多不同之处。
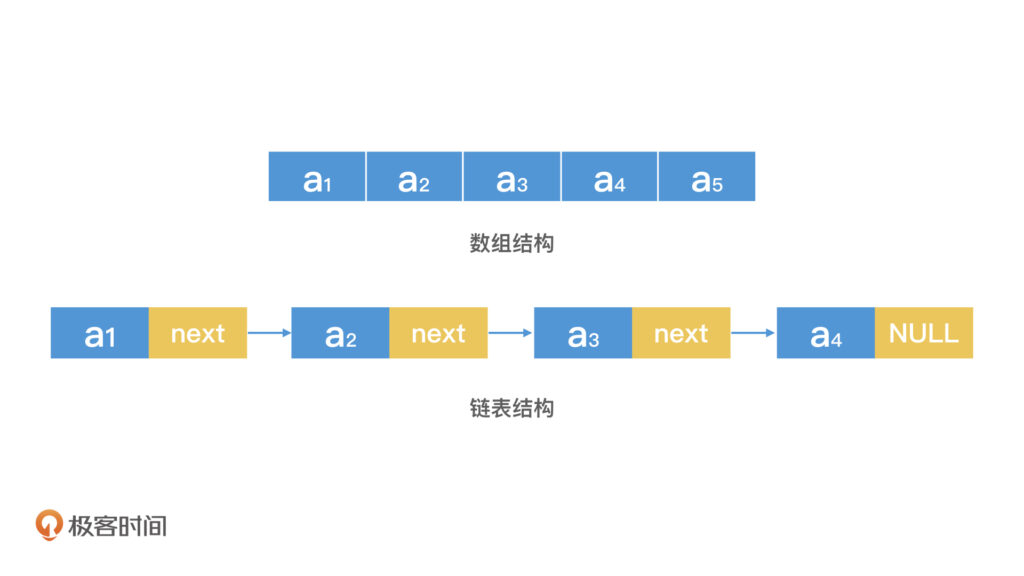
从存储方式来看,数组是一种连续的存储结构。它在内存中占用一块连续的空间,所有元素按照顺序依次存储。例如,一个整数数组,假如数组的第一个元素存储在内存地址为 1000 的位置,每个元素占用 4 个字节的空间,那么第二个元素就存储在 1004 的位置,第三个元素存储在 1008 的位置,依此类推。这种连续存储的方式使得数组可以通过索引快速访问元素。如果要访问数组中的第 n 个元素,只需要知道数组的起始地址和每个元素的大小,就可以通过简单的计算(起始地址 + n * 元素大小)来获取元素的存储位置。但是,数组的大小在创建时就需要确定,一旦确定后就很难进行扩展。如果要扩展数组的大小,通常需要重新分配一块更大的连续内存空间,然后将原来的数据复制到新的空间中。
链表则是一种非连续的存储结构。链表由一系列节点组成,每个节点包含数据部分和指向下一个节点的指针(在单链表中)。节点在内存中的位置可以是不连续的。例如,第一个节点存储在内存地址为 2000 的位置,它的下一个节点可能存储在 3000 的位置。链表的这种结构使得它在插入和删除元素时比较灵活。如果要在链表中插入一个新节点,只需要调整相关节点的指针即可。比如,要在节点 A 和节点 B 之间插入一个新节点 C,只需要将节点 A 的指针指向节点 C,然后将节点 C 的指针指向节点 B。但是,链表访问元素的效率相对较低。如果要访问链表中的第 n 个元素,需要从链表的头节点开始,逐个遍历节点,直到找到第 n 个节点,这在链表长度较长时会比较耗时。
在空间使用方面,数组由于是连续存储,可能会存在空间浪费的情况。比如,你创建了一个长度为 10 的数组,但是只使用了其中的 5 个元素,那么剩下的 5 个元素所占用的空间就被浪费了。而链表则是根据实际需要动态分配每个节点的空间,不存在这种空间浪费的情况。不过,链表因为每个节点都需要额外的空间来存储指针,所以在存储相同数量的数据时,链表所占用的总空间可能会比数组多。
从应用场景来看,数组适合于需要频繁访问元素,并且数据量相对固定的情况。比如,存储一个班级学生的成绩,成绩的数量通常是固定的,而且经常需要根据学号(索引)来查询成绩,这时数组就是一个很好的选择。链表则适用于需要频繁插入和删除元素的情况。例如,一个动态的任务队列,任务不断地被添加和移除,使用链表可以更高效地实现这种操作。
你最喜欢哪些排序的算法。如果我是一个完全不懂的人,请你向我介绍一下它(如堆排序、快速排序) ?
我比较喜欢快速排序和堆排序。
先来说说快速排序。快速排序的基本思想是通过一趟排序将待排记录分割成独立的两部分,其中一部分的所有记录均比另一部分的所有记录小,然后再分别对这两部分记录继续进行排序,以达到整个序列有序。
想象一下,你有一堆数字卡片,你先从这堆卡片中随便选一个数字,把它作为一个 “基准”。然后把所有比这个基准小的数字放在它的左边,所有比这个基准大的数字放在它的右边。这样,这堆卡片就被分成了两小堆。接着,你对这两小堆卡片再分别重复刚才的操作,一直到每小堆里面只有一个或者几个已经排好序的数字为止。
例如,有数组 [5, 3, 8, 4, 7],我们选择 5 作为基准。从数组的两端开始扫描,先从右边找一个比 5 小的数,找到 4,再从左边找一个比 5 大的数,找到 8,交换 4 和 8 的位置。接着继续扫描,找到 3 比 5 小,7 比 5 大,交换 3 和 7 的位置。最后把基准 5 和左边的 3 交换位置,这样就得到了 [3, 4, 5, 8, 7]。然后对 3 和 4 这部分以及 8 和 7 这部分分别进行同样的操作,直到整个数组有序。
快速排序的平均时间复杂度是 O (n log n),这在处理大量数据时是非常高效的。但是在最坏的情况下,时间复杂度会退化成 O (n²),这种情况比较少见,通常是在数据已经有序或者接近有序的时候。
再讲讲堆排序。堆排序是利用堆这种数据结构来进行排序的方法。堆是一种特殊的完全二叉树,分为大顶堆和小顶堆。大顶堆的每个节点的值都大于或等于它的子节点的值,小顶堆则相反。
以大顶堆为例,我们先把要排序的数据构建成一个大顶堆。就像堆一个金字塔,最大的数字在最上面。然后把堆顶的元素(也就是最大的元素)和最后一个元素交换位置,这样最大的元素就被放到了数组的最后。接着,我们把剩下的元素重新调整为大顶堆,再把堆顶元素和倒数第二个元素交换位置,依此类推,直到整个数组有序。
假设我们有数组 [4, 6, 8, 5, 7],首先将它构建成大顶堆。经过调整后得到 [8, 7, 6, 5, 4]。然后交换 8 和 4,得到 [4, 7, 6, 5, 8],再对前面 4 个元素重新调整为大顶堆,重复这个过程,直到数组有序。堆排序的时间复杂度是比较稳定的,为 O (n log n),而且它是一种原地排序算法,不需要额外的存储空间。












暂无评论内容